A Bayesian network approach for cybersecurity risk assessment implementing and extending the FAIR model
使用贝叶斯网络来扩展公平模型(fair model),定量风险评估
已有工作
FAIR用于评估智能电网网络威胁的损失事件频率,2019
Park等人使用FAIR来评估Andriod恶意软件的威胁,2018
典型的CRA(风险评估)方法
- 威胁树,2002
- 攻击树,1999
- 攻击图,2002
- 防御树,2006
- 贝叶斯攻击图,2012
博弈论模型存在的问题
信息的缺乏和不对称:
- 不知道攻击者的策略和payoff
- 很难指导风险管理者进行决策和评估
考虑将博弈模型和统一收益模型相结合:将博弈论模型和FAIR-BN相结合,可以支持防御者-攻击博弈中防御者部署的决策,并预测网络攻击造成的损失。
博弈模型
借用Banks,2015的序列防御-攻击博弈模型来构建EFBN
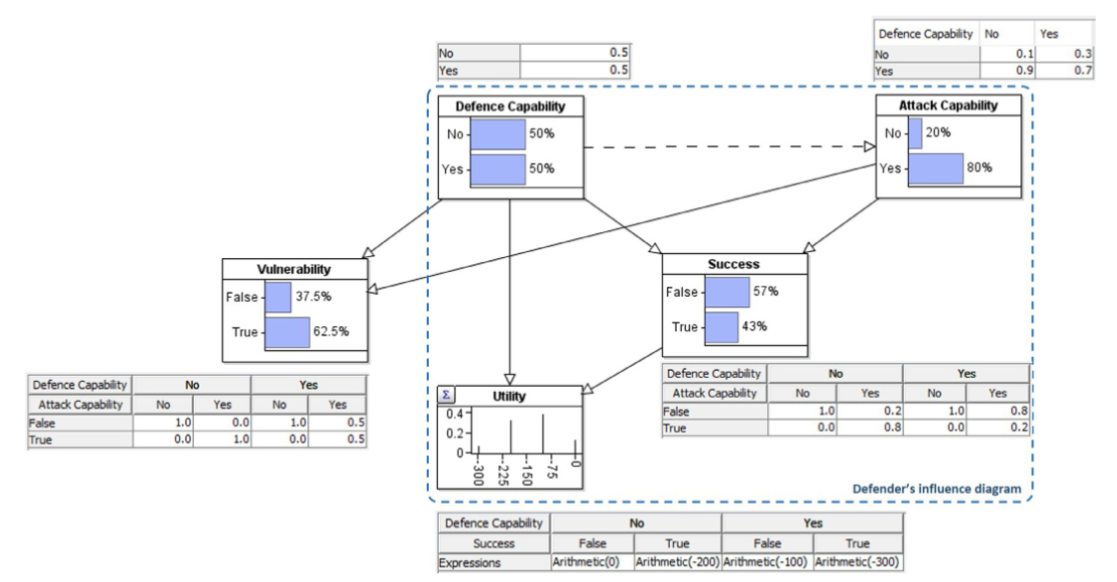
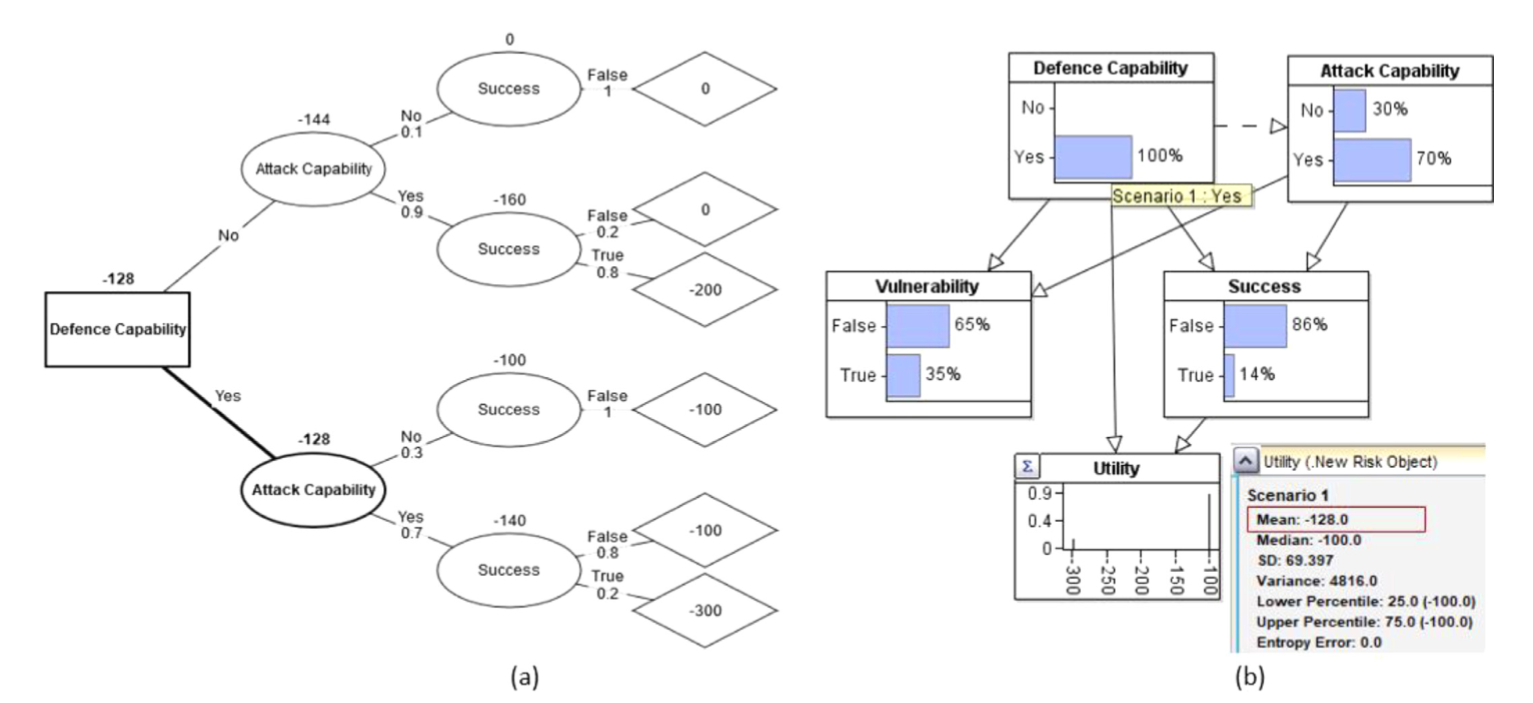
决策分析的目标是使得决策者的效用节点最大化,可以使用AgenaRisk生成决策树(Fenton,Neil,2018)
A Hybrid Game Theory and Reinforcement Learning Approach forCyber-Physical Systems Security
基于博弈论和多智能体强化学习在战略和战场两个维度去考量。
- 使用预定义漏洞和已发现漏洞
- 使用MARL和Q-learning推导最有攻击序列和防御策略
背景
MARL(多代理agent强化学习) [6]被认为是博弈论的改编,具有机器学习的附加功能,可以使用深度强化学习在内的多种算法来学习最优策略,也就是收敛到nashEQ
强化学习案例:
- R. Elderman, L. J. Pater, A. S. Thie, M. M. Drugan, and M. Wiering,“Adversarial reinforcement learning in a cyber security simulation.,” inICAART (2), pp. 559–566, 2017
- . Huang, C. Zhou, Y. Qin, and W. Tu, “A game-theoretic approachto cross-layer security decision-making in industrial cyber-physicalsystems,”IEEE Transactions on Industrial Electronics, 2019.
模型
战略层面
我们使用不完善的信息广泛形式博弈对战略水平进行建模。 此游戏的状态为总体安全状态:低,中,高和严重危险。 显然,防御者不确定确切的状态是什么(例如,攻击者发现了零日漏洞)。 攻击者不知道状态是什么,因为他没有有关目标网络的全部信息或所有防御者的对策。 因此,我们认为信息模型不完善。 该游戏具有扩展形式,因为防御者将尝试从腐败状态恢复到原始(低)状态。攻击者将尝试达到关键状态。 因此,游戏具有多个阶段。 防御者根据对策选择策略,以阻止攻击者的前进。 该策略被转化为一系列在战场上可以选择的行动。 攻击者根据攻击方法选择策略。 攻击者策略被翻译为战场级别的一组动作,漏洞和渗透工具。
战场层面
采用MARL。包含一个主机和四个子网构成的CPS
- 三个子网在云端,拥有IDS。安全影响较低
- 其它子网托管在本地,IDS具有不确定性易受到攻击。中等的影响
- SCADA网络,具有高安全性影响。
漏洞评分系统(CVSS):“Common vulnerability scoring system.” https://www.first.org/cvss/. Ac-cessed: 2019-08-02
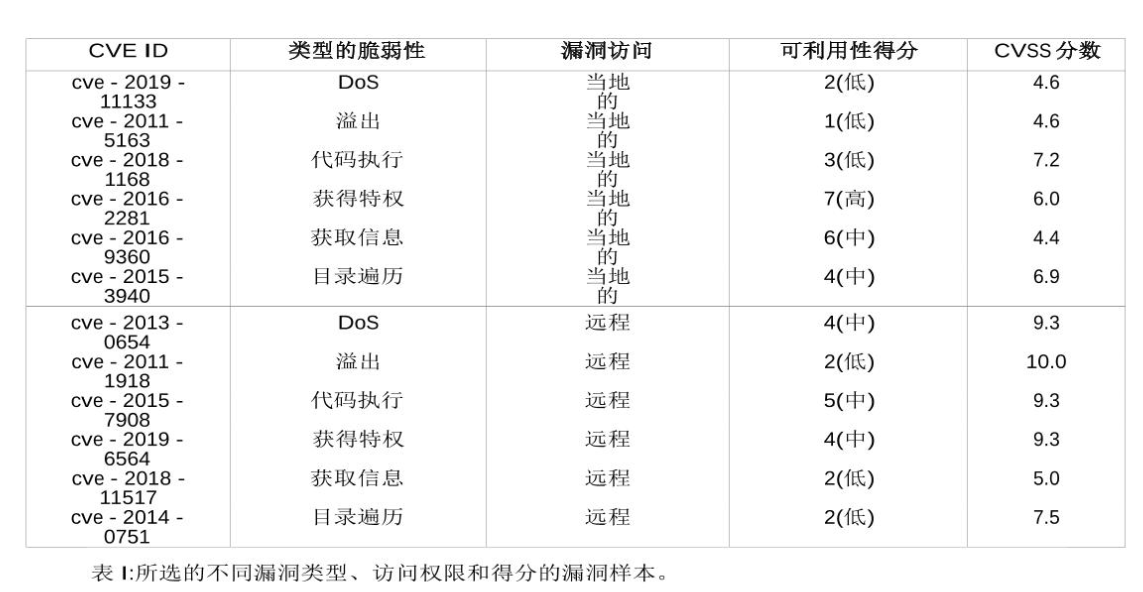
一个典型的CPS子网有关的漏洞。
病毒传播模型
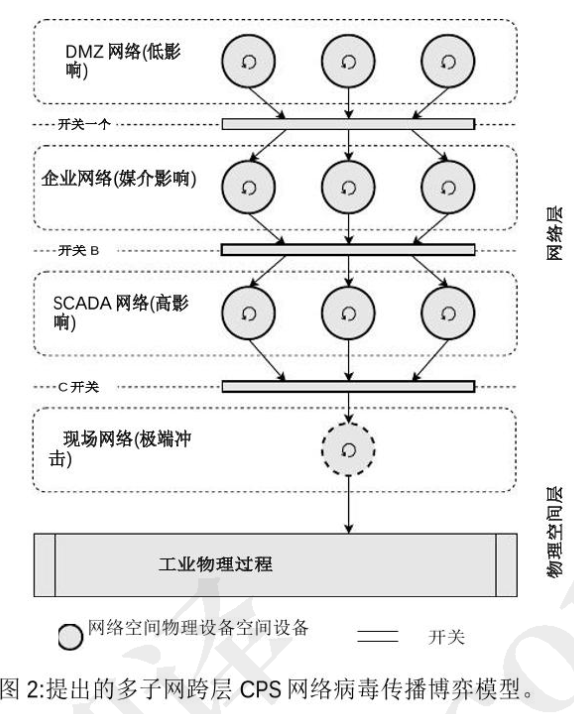
攻击者在攻击过程收集信息。
描述
首先使用基于Q-learning的RL寻找最优攻击路径;进一步,将MARL处理Q-learning应用于两个agent以到达NE,并找到最佳防御策略
博弈法制
使用以下6元组定义:14x6game model matrix (14 nodes, five vulnerabilities, level ofprotection)
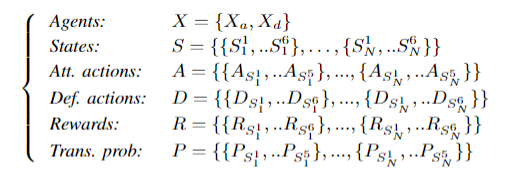
- 参数 $W$ :如果IDS检查到病毒,返回1,否则返回0
- 参数 $T$:是否终止
- 参数 $Y$:攻击者的步长
- 参数 $V$:攻击成功率
- 参数 $N$:最后一个节点的index
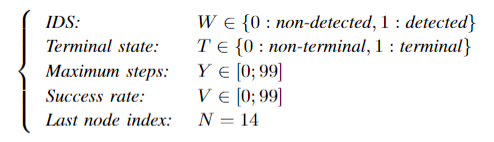
攻击者的目标状态:
攻击成功率 $V$ 应超过漏洞可利用性得分 $P$,形式化描述为:
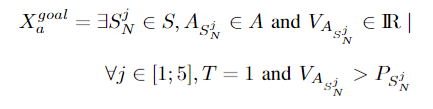
防御者目标状态:
对于防御者的目标状态,在两种情况下游戏被认为是吉祥的:首先,只要攻击者的行动成功不超过最后节点上的转移概率,并且IDS检测到攻击,然后将其阻止; 第二,超过最大攻击步数时,形式化描述:
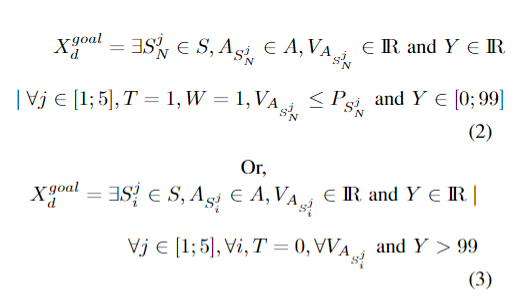
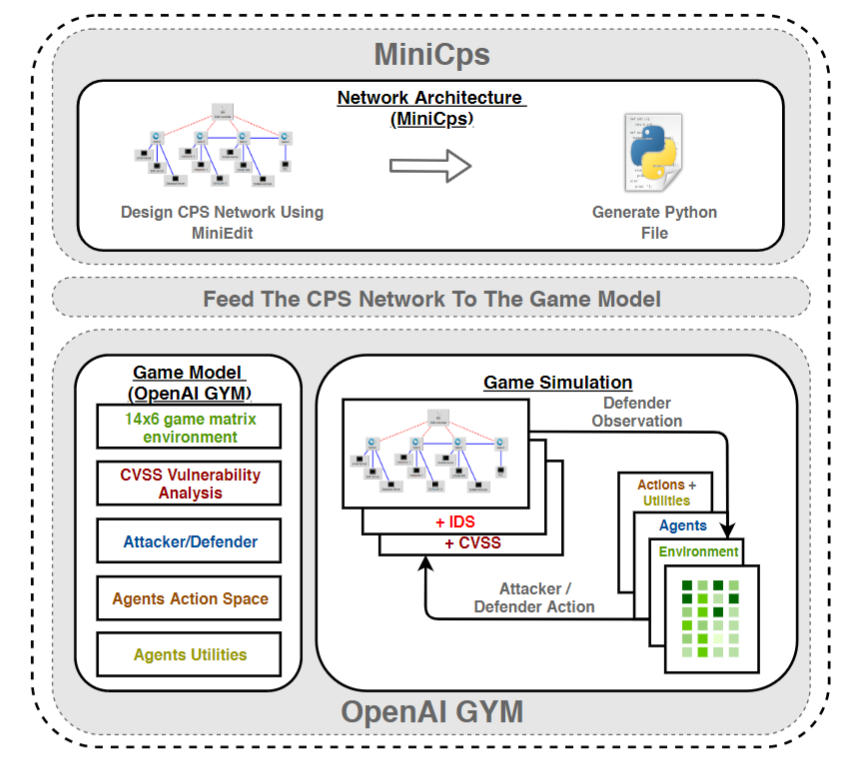
架构图
学习算法基于table表示法而不是神经网络,因为神经网络存在对抗性学习问题,即对不断变化的环节适应很慢。
学习参数
- 学习率:描述新值和旧值的比较程度
- 折现因子:影响未来奖励的权值。
- 衰减率:确定勘探与开发之间的权衡。
Q-tables会在每个game策略中更新。
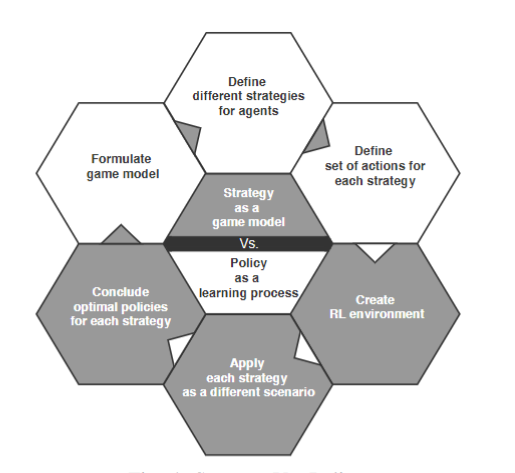
战略与策略
图4给出了使用博弈论和 MARL的想法;它将博弈论中的策略概念与RL 中的政策概念联系起来。首先基于博弈论原理对 CPS网络中所面临的问题进行建模和形式化。每个玩家都定义了相应的策略和行动空间。同时,通过使用MARL,将博弈模型的形式化应用到环境中,使用Q-learning算法来应用学习过程。此外,对所选择的策略推导出最优策略。